Consensus in the IOTA Tangle — FPC

This is the first in a series of posts that explain the consensus protocols described in IOTA Coordicide.  

The main objective of this series is to keep the community updated on recent research results and also to explain interesting research questions having good chances to be funded by Coordicide grants. As you will see, the topic is quite vast and there are a lot of connections and dependencies on other parts of the Coordicide project.  

Faced with this complexity, we’ll try to explain only a few points at a time and focus on questions that are currently being researched. That said, let us note that IOTA already has all the key ingredients for an efficient and secure solution for Coordicide.

The remaining questions are about optimality of the solution, for instance:

1. Increasing safety
2. Increasing sustainability (e.g. decreasing message complexity, decreasing PoW)
3. Increasing TPS
4. Decreasing time to finality
5. Increasing the flexibility of the implementation for challenges in the future

Now, let’s get down to it and understand what this “consensus” is all about.

Why consensus?

Distributed consensus algorithms allow networked systems to agree on a required state or opinion in situations in which decentralized decision making is difficult or even impossible.

Distributed computing is inherently unreliable. Achieving consensus enables a distributed system to work as one entity. The importance of this challenge stems from its omnipresence in which fault tolerance is one of the most fundamental aspects.

Common examples include: replicated file systems, clock synchronization, resource allocation, task scheduling and last, but not least, distributed ledgers.

Distributed systems form a vast and classic topic in computer science and the same is true for associated consensus protocols: see How does distributed consensus work for an elegant introduction to this topic.  

The existing consensus protocols are essentially the classical protocols — e.g. those based on PAXOS — and the recent game-changer:the Nakamoto consensus. Both protocols have serious restrictions.

The classical protocols have quadratic message complexity, they require precise membership knowledge and are rather fragile against disturbances. The Nakamoto protocol, on the other hand, is robust and does not require precise memberships. However, it relies on PoW, leading to well-known problems such as mining races and non-scalability.

So how is consensus achieved in the IOTA Tangle?

Let us first look back at the Nakamoto consensus. One brilliant idea of the Nakamoto consensus is to make the consensus non-deterministic or probabilistic. Instead of all nodes of the (distributed) system agreeing on the correctness of a value, they agree on the “probability” of that value being correct.

The role of the leader in traditional consensus protocols is taken by the node that solves a given computational puzzle the fastest; this winner adds a new block to the blockchain. This way, the (distributed) network is building the ever-growing blockchain and agrees on the validity of the longest chain or the chain with most cumulative difficulty.

So why is this consensus probabilistic? In order to know that a certain transaction will be considered valid, in say 100 days, we have to know that the longest chain in 100 days will contain this given transaction.

In other words, we are interested in the probability that the longest chain in 100 days will contain this transaction. The probability that a transaction will not be reverted increases as the block which contains this transaction sinks “deeper” into the chain.

In the bitcoin blockchain, for example, it is recommended to wait until a transaction is six blocks deep in the blockchain. After this depth, the probability that a transaction is reverted is very low.

This effect also applies to the Tangle. The deeper — or more “enveloped” by the Tangle — a transaction gets the more final it becomes. In the following picture, the dark green transaction is validated by all light green transactions. As the number of light green transactions grows, the probability of the dark green transaction being in the future Tangle converges to 1.

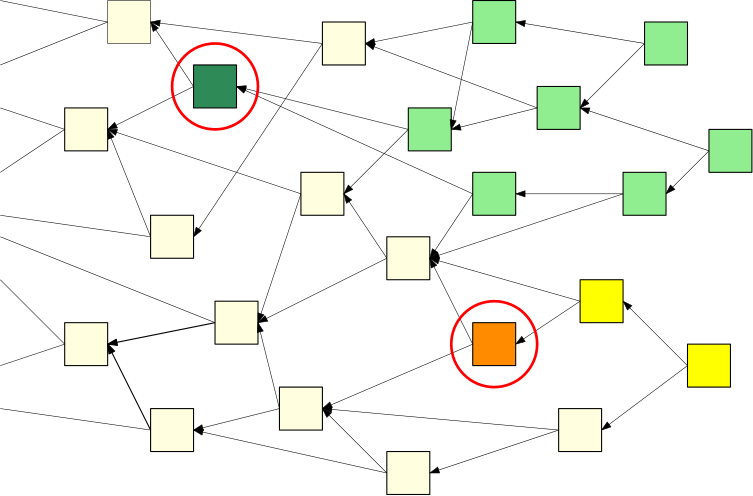
But wait, the Tangle is different to a blockchain!While the blockchain is not allowed to contain two conflicting transactions, the Tangle may temporarily contain such transactions. Therefore, it may be that a malicious player attaches two conflicting transactions at different parts of the Tangle, like the dark green and the orange squares in the above picture.  

These transactions may “survive” in the Tangle for a short time until honest nodes detect the conflict. Once such a conflict is detected, the nodes decide on which transaction to choose. In the example above, the darker green transaction is “more enveloped” by the Tangle and should eventually be approved by all nodes.

For the Tangle to become a real consensus protocol we have to decide on conflicting transactions. That decision should be taken by using a consensus protocol.

Did we walk in circles here?? Fortunately no: Coordicide proposes two other consensus protocols:

• the fast probabilistic consensus(FPC) and
• the cellular consensus(CC)

The rest of this post will be devoted to a short introduction to FPC and to explain how to reach consensus when it comes to deciding whether a single transaction is valid or not.

In a future blog post, we will address why this is sufficient in order to reach consensus on Tangle level and we will discuss the finality of transactions in the Tangle.

What is FPC?

In fancy terms, the FPC is a leaderless probabilistic binary consensus protocol of low communicational complexity that is robust in a Byzantine infrastructure — check the original article by Serguei Popov and Bill Buchanan.  

Let us see, as we proceed what all these terms really mean and start by presenting a lighter version of the FPC that is easy to implement and contains most of the important features.

We assume the network to have n nodes indexed by1,2,…,n. Every node i has an opinion or state. We denotes_i(t)for the opinion of the node i at time t. Opinions take value in{0,1}; being the reason we speak of a binary consensus.  

The basic idea is majority voting. At every round, every node queries k random nodes and sets its opinion equal to the majority of the queried nodes. Simple as that! However, this simple majority voting turns out to be fragile against faulty nodes and malicious attackers. It needs an additional ingredient, in fact an additional randomness, to make it robust.  

More formally, at each step, each node chooses k random nodes C_i, queries their opinions and calculates the mean opinion  

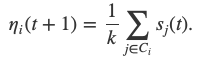
We denote𝝉 ∊ [0,1]the first threshold that allows some asymmetric nature of the protocol, another topic we’ll address in the near future. Furthermore, we introduce an “additional randomness”; letU_{t}, i=1, 2,…be i.i.d. random variables with law Unif (𝜷, 1- 𝜷)for some parameter𝜷 ∊ [0,1/2].  

At each time, each node i uses the opinions from k random nodes to update its own opinion:  

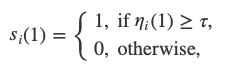
and fort>0:

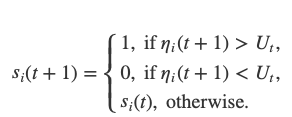
It is important that at each round a node queries a different random set of nodes and that the random variablesU_tare updated in each round as well.

We introduce a local termination rule to reduce the communication complexity of the protocol. Every node keeps a counter variable cnt that is incremented by1if there is no change in its opinion and that is set to0if there is a change of opinion.  

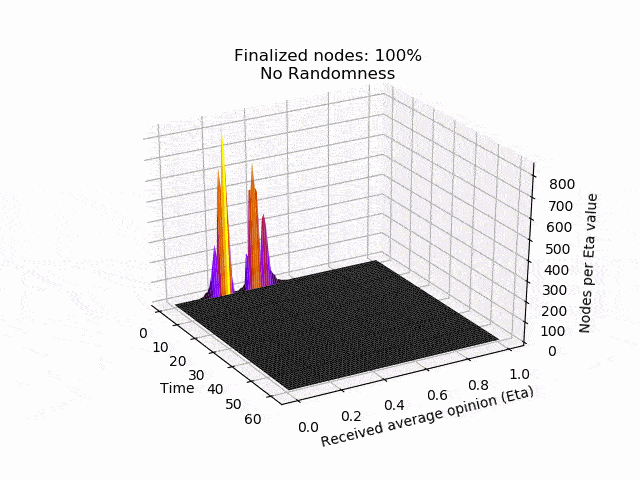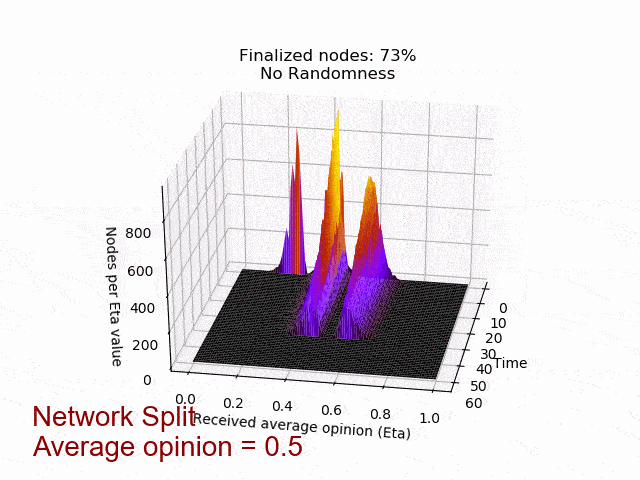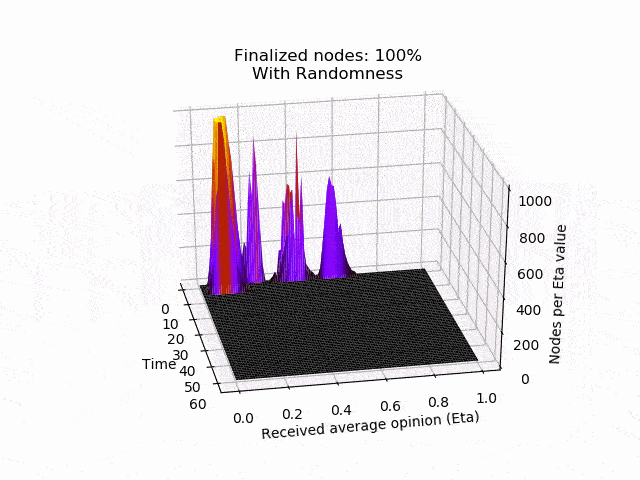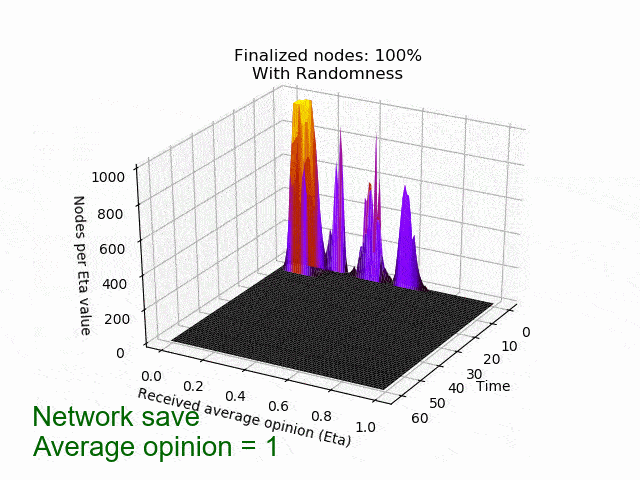
Once the counter reaches a certain threshold l, i.e.cnt ≥ 1, the node considers the current state as final. The node will therefore no longer send any queries, but will still answer incoming queries. The next graphs show typical evolutions of the variable cnt for each node with l=5, k=10and initial opinions of 90% of1`s and 10% of0`s.  

In the left picture the protocol is not disturbed, but in the right picture 20% of the nodes are maliciously trying to turn the majority of the honest nodes. In both cases, eventually all honest nodes agree on the initial majority.

We want to highlight the feature of the common random thresholds of the FPC and refer to Simulation of the FPC for a first analysis of the FPC for various different kinds of parameter settings and attack strategies.  

The importance of uncertainty in war was introduced by Carl von Clausewitz:

War is the realm of uncertainty; three quarters of the factors on which action in war is based are wrapped in a fog of greater or lesser uncertainty. A sensitive and discriminating judgment is called for; a skilled intelligence to scent out the truth.

War is the realm of uncertainty; three quarters of the factors on which action in war is based are wrapped in a fog of greater or lesser uncertainty. A sensitive and discriminating judgment is called for; a skilled intelligence to scent out the truth.

- Carl von Clausewitz, 1873

What does this have to do with the random thresholds in the FPC? In simple majority, voting these thresholds would just be equal to0.5. A fruitful attack strategy could be to keep theη’s of the honest nodes around0.5preventing a convergence of the protocol (we will see such a successful attack later on). The idea of Popov and Buchanan was to add “noise” or “fog” to the system to increase the uncertainty of information for the potential attackers.

Why is all of this important? In a situation without malicious nodes, the distribution of theη’s will be close to a normal distribution:

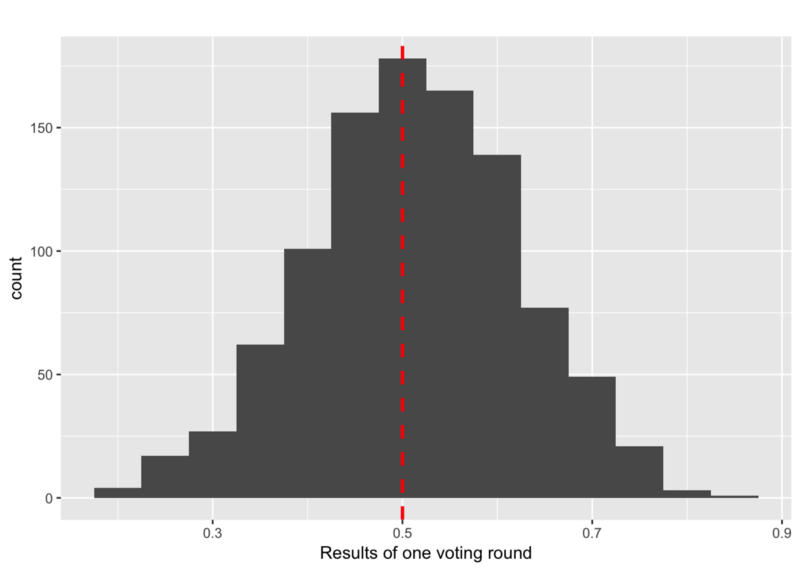
Already in a non-disturbed situation, the opinions of the honest nodes can stay close to a 50:50 situations. However, random effects, caused by the random voting, finally lead to convergence of the protocol. This situation is completely different in a Byzantine infrastructure.

Let’s consider an adversary strategy that subdivides the honest nodes into two equally sized groups of different opinions leading to a distribution of theη’s among honest nodes like:

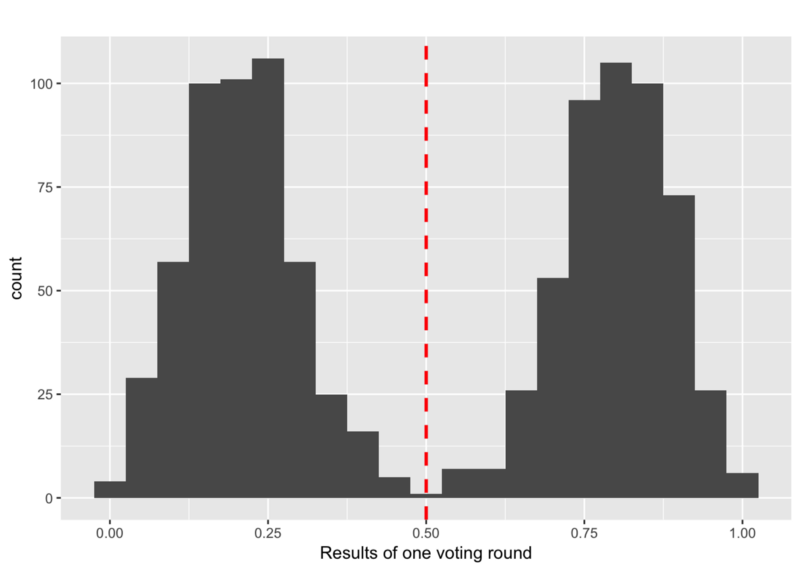
So how can an adversary achieve this?

The adversary waits until all honest nodes have received opinions from all other honest nodes. The adversary then calculates the median of these intermediateη’s. Now, the adversary tries to keep the median of theη’s close to0.5by trying to maximize the variances of theη’s.  

How can the FPC prevent such an attack? By replacing the deterministic threshold (red, dashed) by random thresholds (blue, dashed). In the following graph, each blue line stands for a random threshold of a given round. As these thresholds are random the adversary cannot foresee how to split the honest nodes in order to keep the 50:50 situation. The best way is to still split them around the value0.5.

However, once a blue line (in r3 in the picture below) is far enough away from the red line, the adversary loses control of the honest nodes and the protocol terminates.

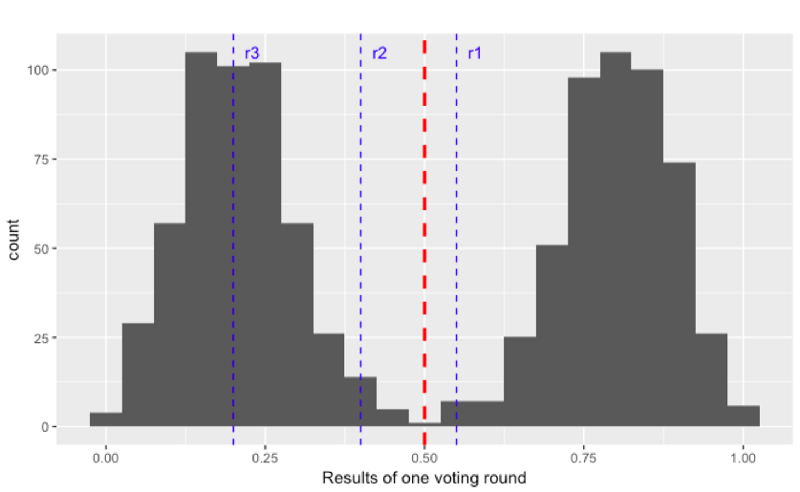
In the following animation you can see the behaviour and outcome of the protocol when this adversarial strategy is applied with no randomness (threshold=0.5) and after the randomness is added. As you can see, the adversary manages to keep the nodes in limbo for an extensive amount of time. But even worse, the network is split in its opinion — leading to an agreement failure. However, after the additional randomness is introduced, the protocol concludes quickly and in unity.

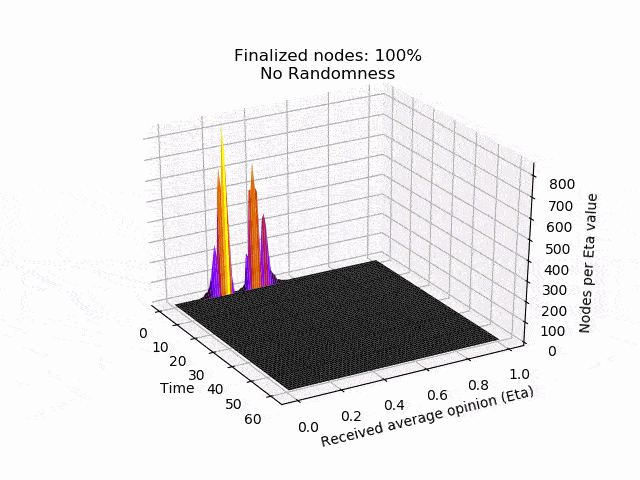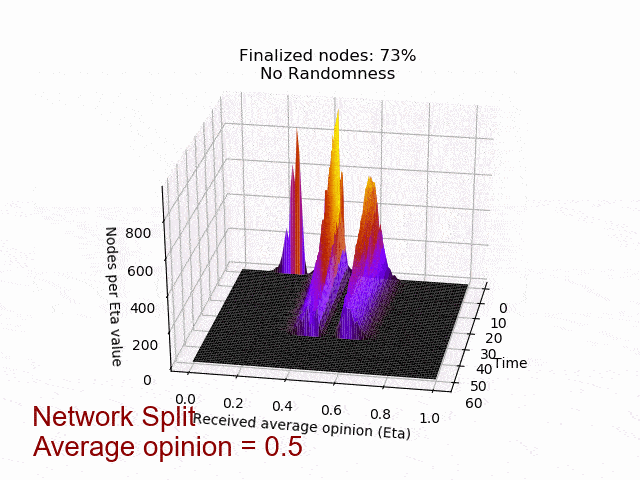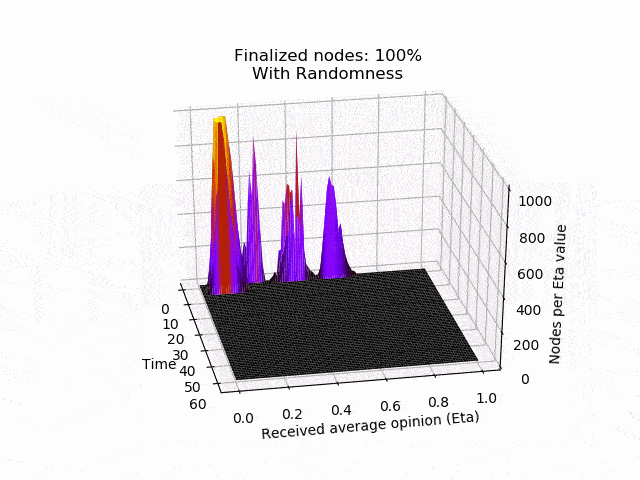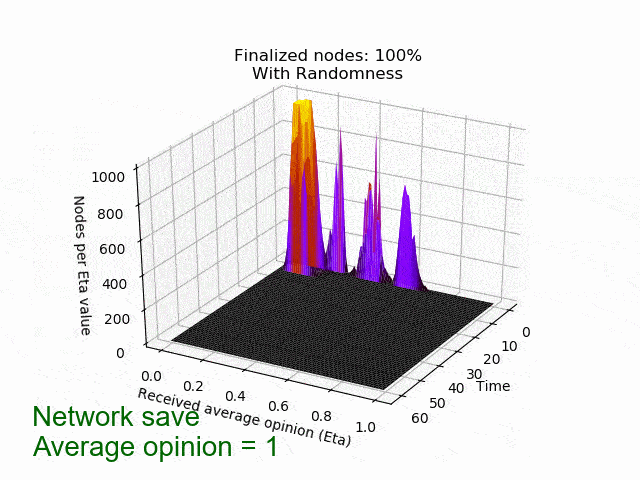
Ongoing work and next steps

Last — but not least — let’s come back to some of the points IOTA is currently working on and point out some examples of future collaborations:

1. At the moment we are running thorough simulations to study various attack strategies on different kinds of network topologies. The results will allow us to identify the optimal amount of randomness and choice of the protocol parameters. We are also investigating robustness of the FPC against failures and disturbances of the random threshold.
2. The bounds on the convergence of the FPC obtained in simulations are far better than the ones obtained theoretically by Popov and Buchanan. Various parameter setting simulations show that there is a so-called “cut off phenomenon”. Informally, this essentially means that the protocol needs, say m steps, with high probability to reach consensus and that it is very unlikely that the protocol needs more than m steps. Theoretical results in this direction would be much appreciated.
3. The actual implementation of the FPC will depend on the reputation of the nodes. As the reputation or mana of the node plays a prominent part in other parts of the Coordicide project, we will write more about this in a future blog post. Anyway, this additional feature will make the protocol safer against various kinds of attacks.
4. The parameters studied above in the FPC were set in stone at the beginning of the protocol. However, in order to increase safety and, at the same time, reduce message complexity (which sounds like a miracle), we are investigating adapted versions of the FPC. For instance, if a node’sηis close to0.5, the node might decide to increase the number of queries while, if it is close to1, it may decide to either reduce the number of queries of the next step or immediately stop querying at all.
5. Nowadays, machine learning is adopted in a wide range of domains where it shows its superiority over traditional rule-based algorithms. We are planning to use machine learning, not only for the detection of faulty and malicious nodes, but also to identify the most harmful attack strategies using reinforcement learning.

We look forward to taking you with us on the exciting journey of Coordicide through the eyes of the research department and we hope you will enjoy the development on this project as we do.

As always, we welcome your comments and questions either here in the comments or in #tanglemath on our Discord. You can also engage in a more intense scientific collaborations with us and apply for a grant.  

The author is not a member of the IOTA foundation. He wrote this blogpost in collaboration with the members of the IOTA research group.