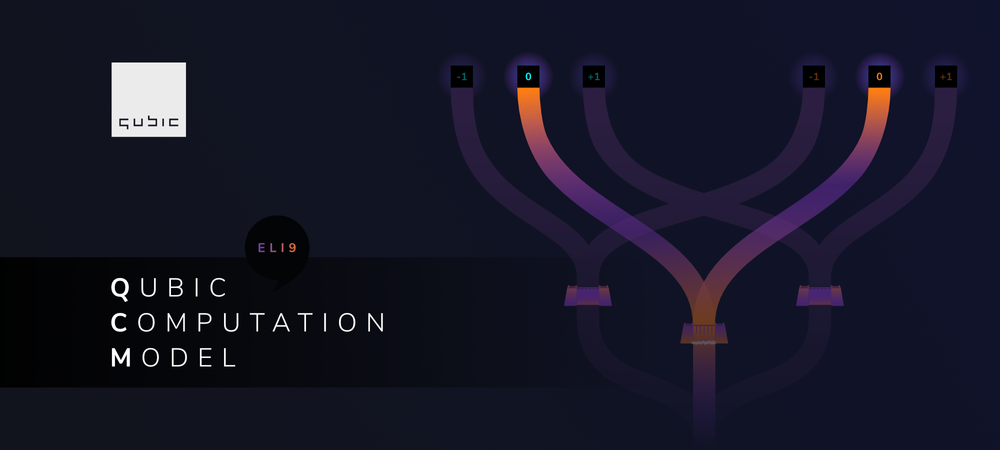
ELI9: The Qubic Computation Model
A simple(r) explanation of the Qubic Computation Model, written following discussions among Andrew Brough, Jake Cahill, Sabri Goldberg, Sergey Ivancheglo, Igor Nielsen, Navin Ramachandran and David Sønstebø. Probably not quite an ELI5.
In this blog post, we will look at how computers work at a basic level, and how we are considering a slightly different approach in Qubic. We call this approach the Qubic Computation Model (QCM).
IOTA aims to enable a machine-to-machine economy, for devices on the Internet of Things. These devices need to work with low amounts of power and in harsh physical environments.
Traditional electronics use complex mechanisms that consume a lot of energy and are more sensitive to these environments. With the QCM we aim to create a more energy-efficient and resilient model for such devices.
QCM traces its origin back to the Jinn Labs project (beginning 2013), looking at novel hardware approaches for Fog/Edge Computing and Distributed Artificial Intelligence. Since that time, the entire semiconductor industry has recognised this new philosophy of “More-Than-Moore”: that the future of computation requires innovative approaches, rather than relying on Moore’s Law for ongoing improvements in computational power.
The QCM initiative holds a special place in IOTA history. It outlined the vision of an organic Machine Ecosystem married with Distributed Ledger Technology, from which IOTA was born.
A computation model describes how a computer works.
A computer takes some data, does some work on it, and returns a result. This process is called a computation, which is at the heart of everything computers do. It’s how computers work out the sum “1 + 1 = 2”. It’s how computers print a letter on the screen when you press a key on a keyboard. It’s how computers do anything.

The path that data takes from the input to the result, through a computation, is called its flow. When we talk about computation models, it’s this flow that we are interested in. Computation models allow us to visualise the flow of data, to find the best way for a computer to reach a result. For example, the model in the video below allows you to input different coins and watch them flow through the channels until they are sorted at the end.
In nearly all computers and digital devices, the traditional computation models requires quite complex mechanisms to handle data flow. The QCM however can handle the flow of data in much cheaper and simpler ways.
Please note that traditional computers work with binary data — all data in binary is represented as a 0 or 1 — these numbers are called bits. QCM works with trinary data — here, the data is represented as a -1, 0, or +1 — these numbers are called trits.
Now, we will start from the basics, to explore how the QCM works and what it is made up of. Then, we will explain how trinary data flows are more efficient than binary ones.
To illustrate how the QCM works, let’s look at a basic computation: How do we check if two different inputs are equal?
For example, if one input is 0 and the other input is also 0, we can conclude that they are equal.
To show how simple it is to build the Qubic Computation Model for this situation, let’s paint a picture that most of us will be familiar with: A sandy beach. Now imagine this beach with:
- Channels in the sand, which represent an electrical circuit
- Channel entrances, into which we can pour water — this represents the data
- Small dams, which represent computations (represented by the dam shapes on the picture below)
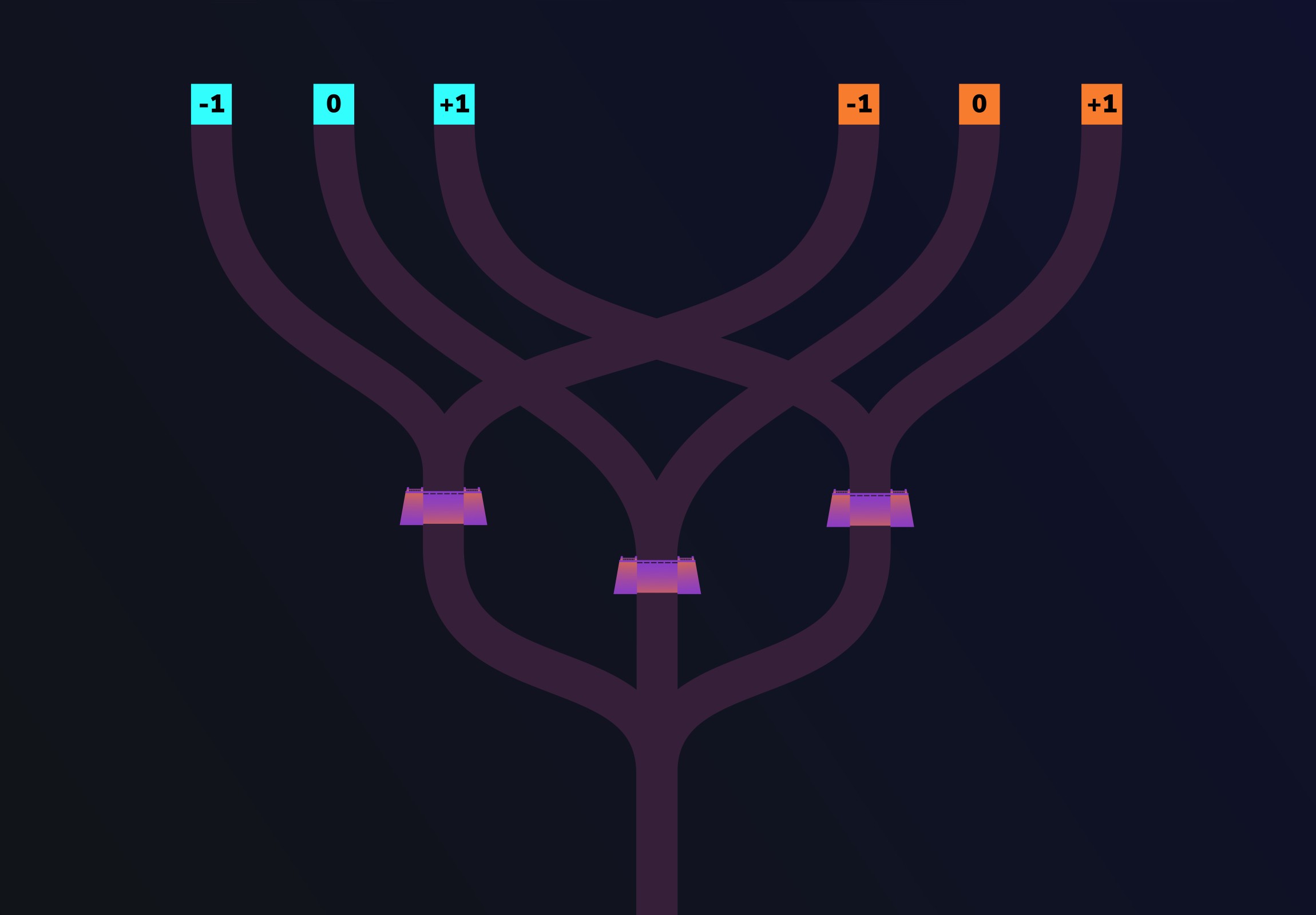
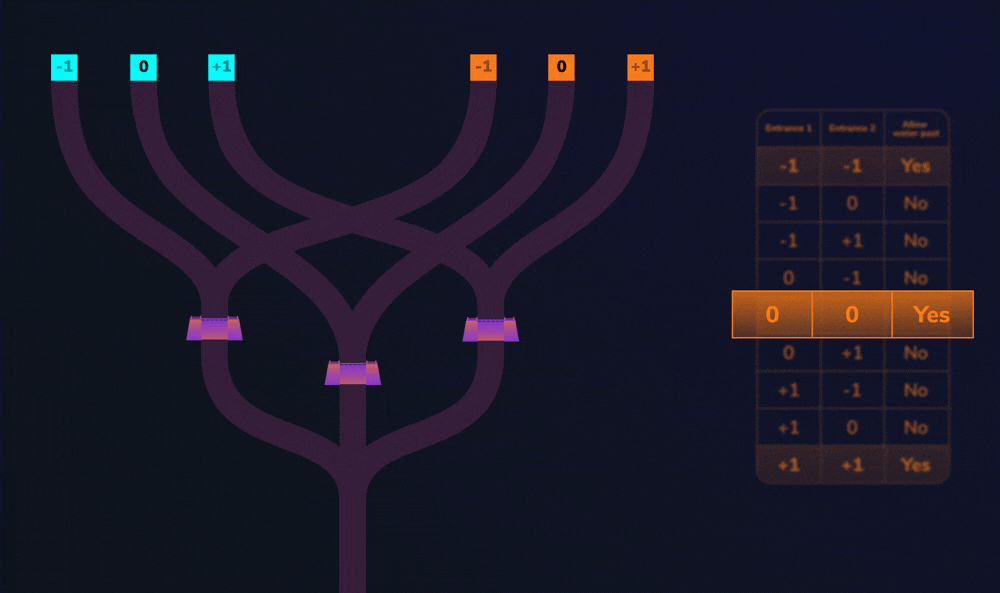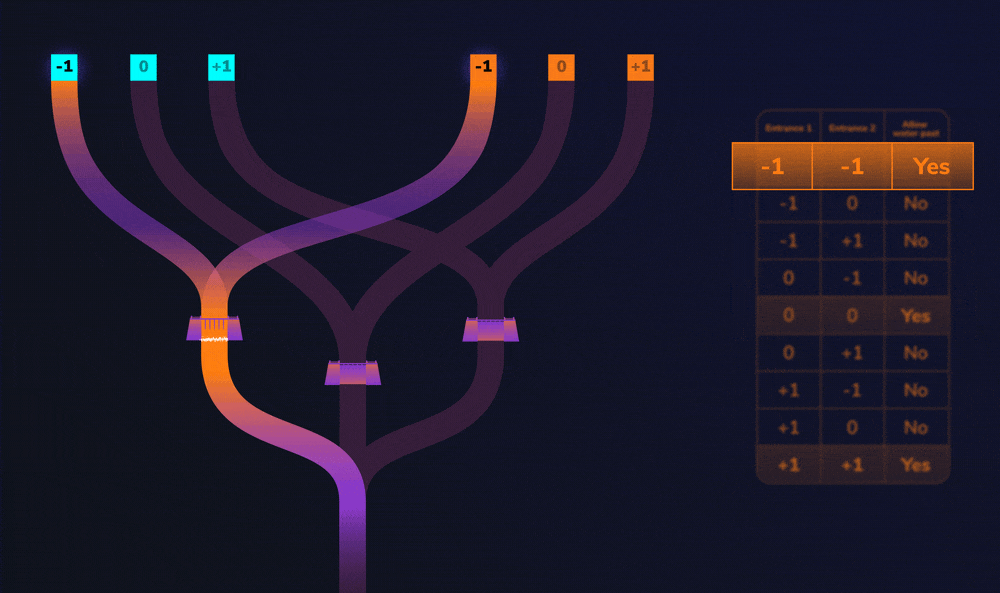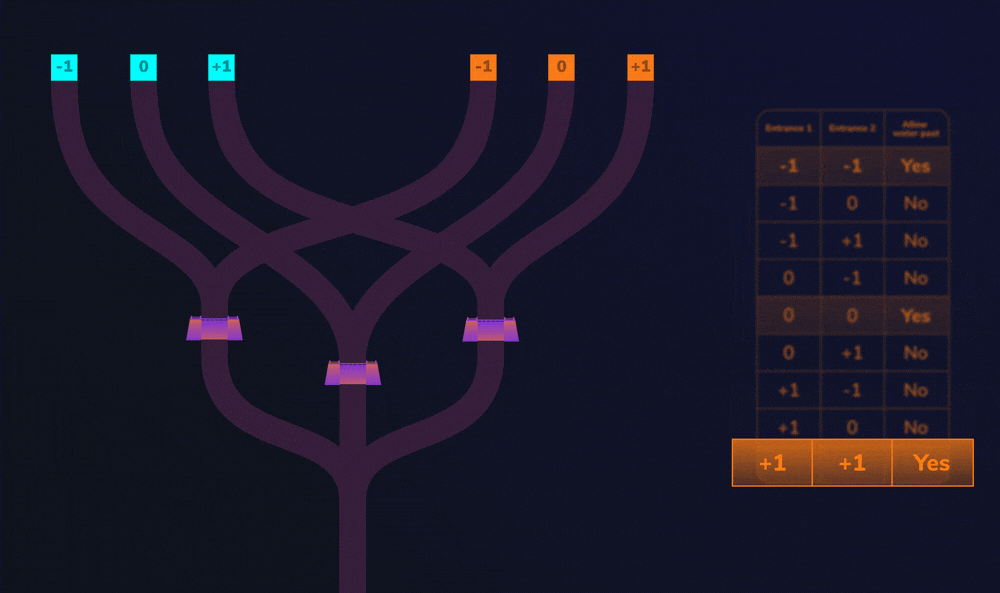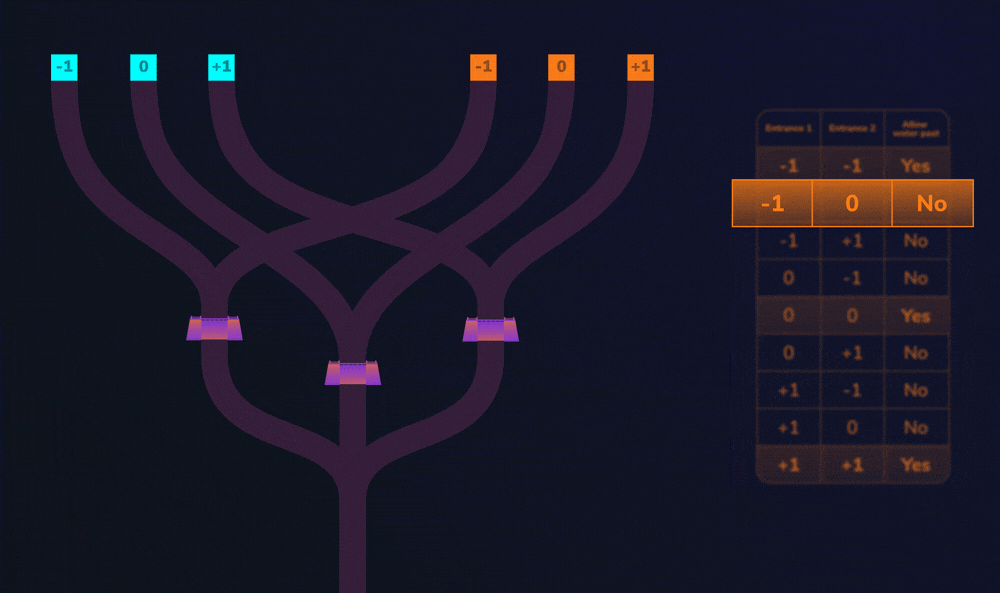
To compare two inputs (cyan and orange), a child (let’s call her Alice) pours water into a cyan entrance and an orange entrance. Both of these entrances can represent one of three values: -1, 0, and +1. Remember these values are called trits.
Now, one channel of water isn’t enough to rise to the top of the dam. So let’s look at 2 different cases.
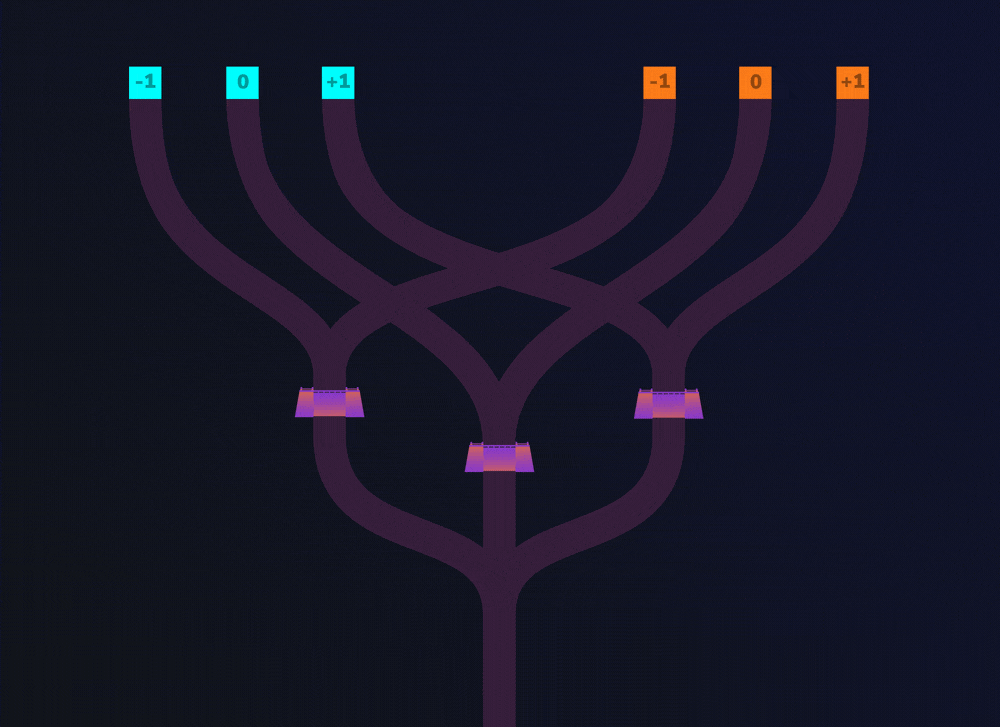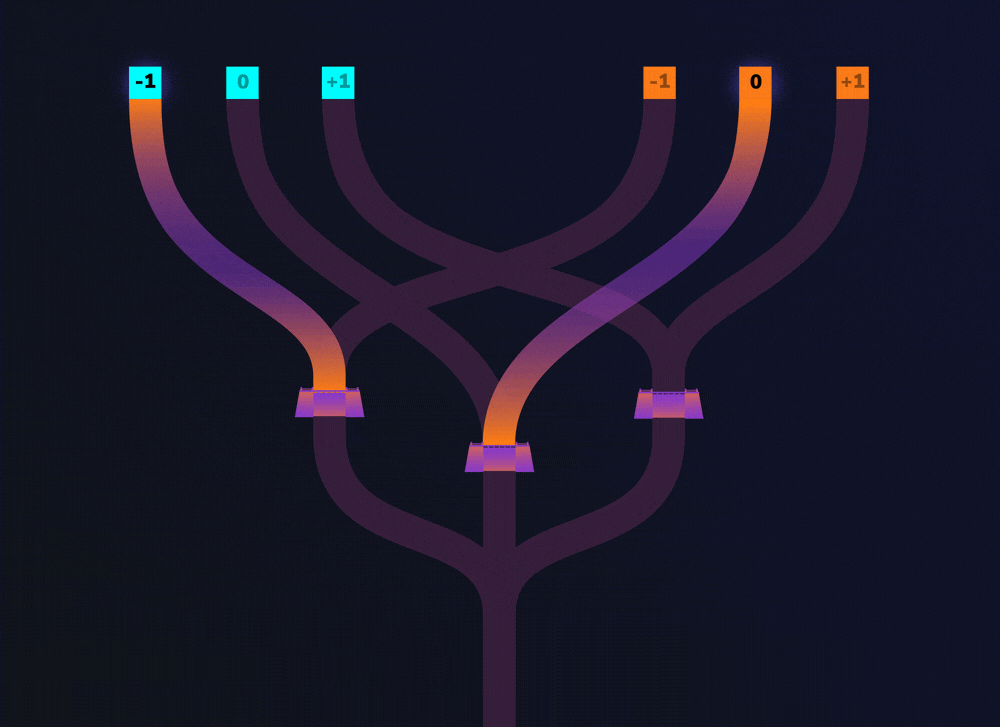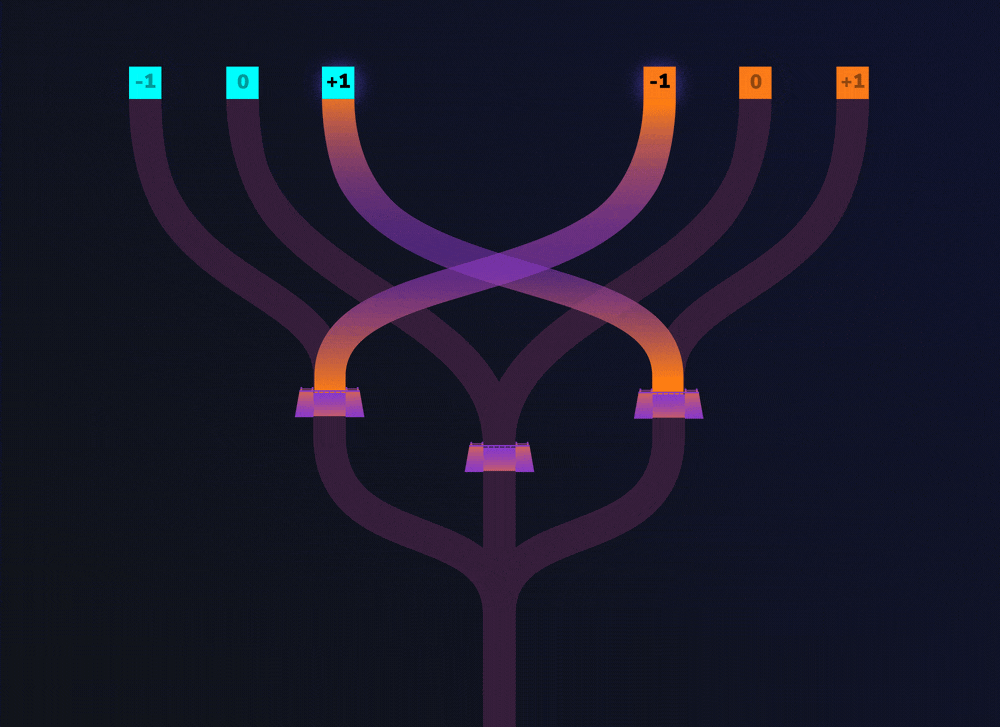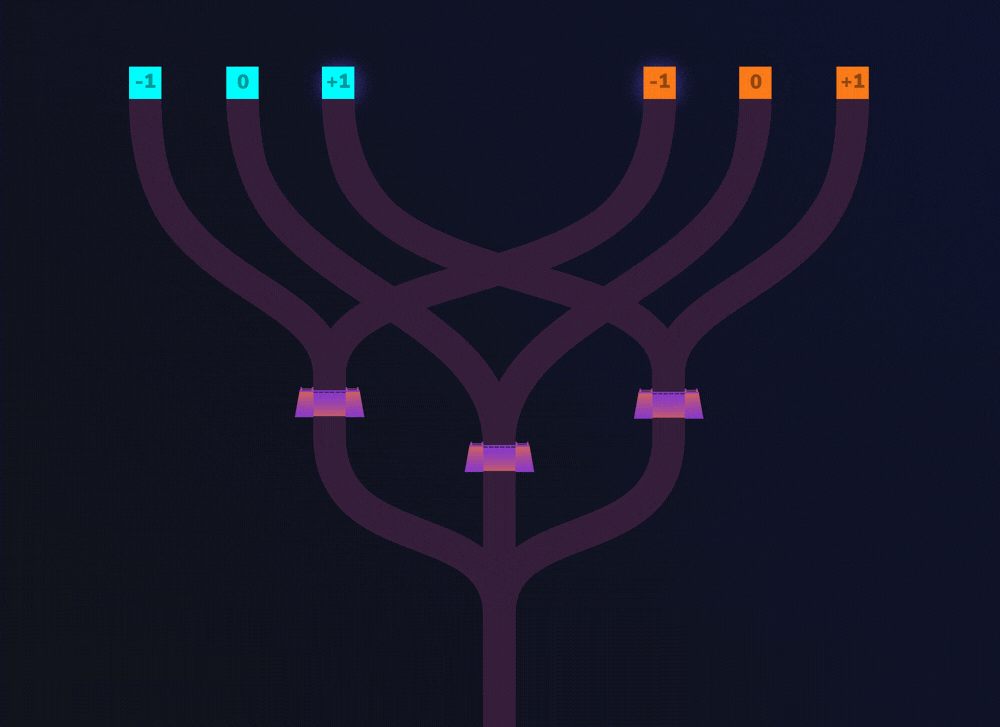
First, imagine that Alice pours water into the 0 trit of the cyan and orange entrances. If you follow the channels from these entrances, you’ll see that both channels lead to the same dam. If both channels lead to the same dam, then enough water rises to the top and flows over it. So, we can say that when water flows over the dam, both input values were the same (0 and 0 in this case).
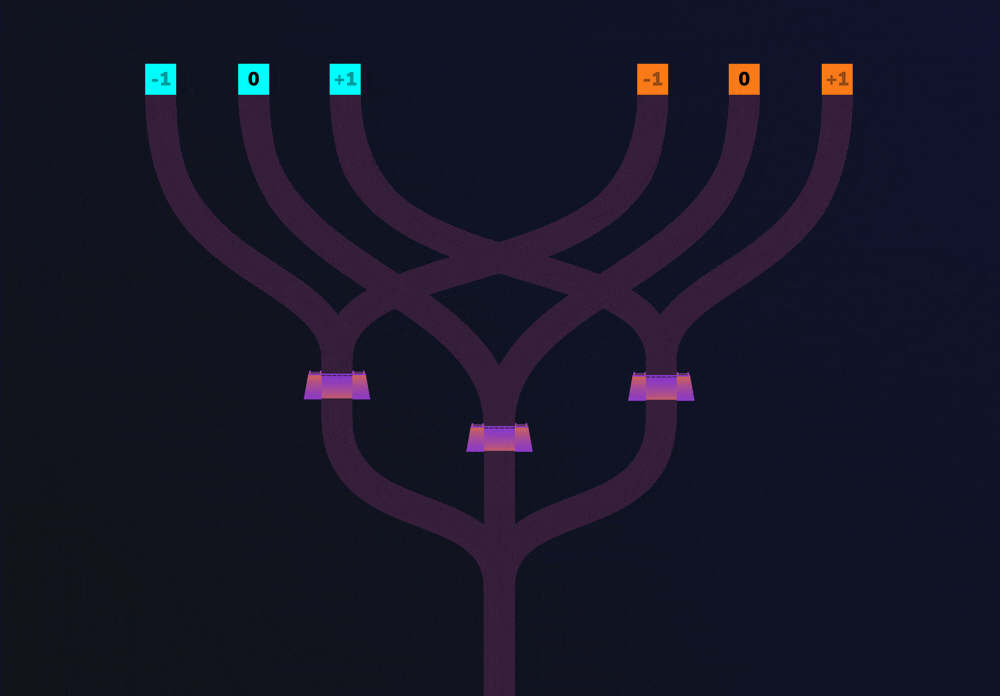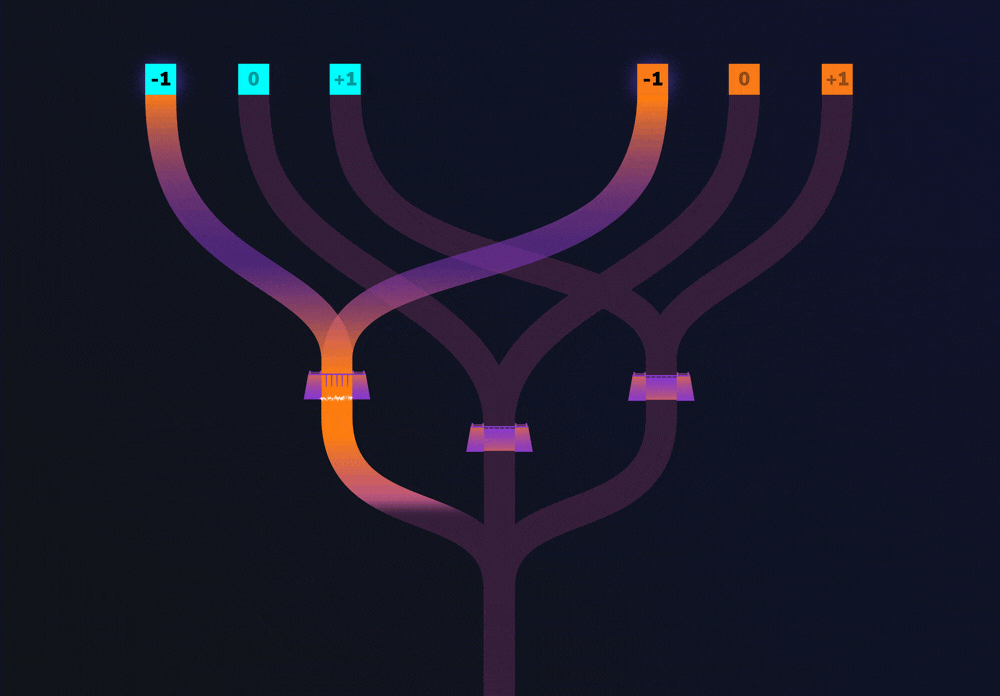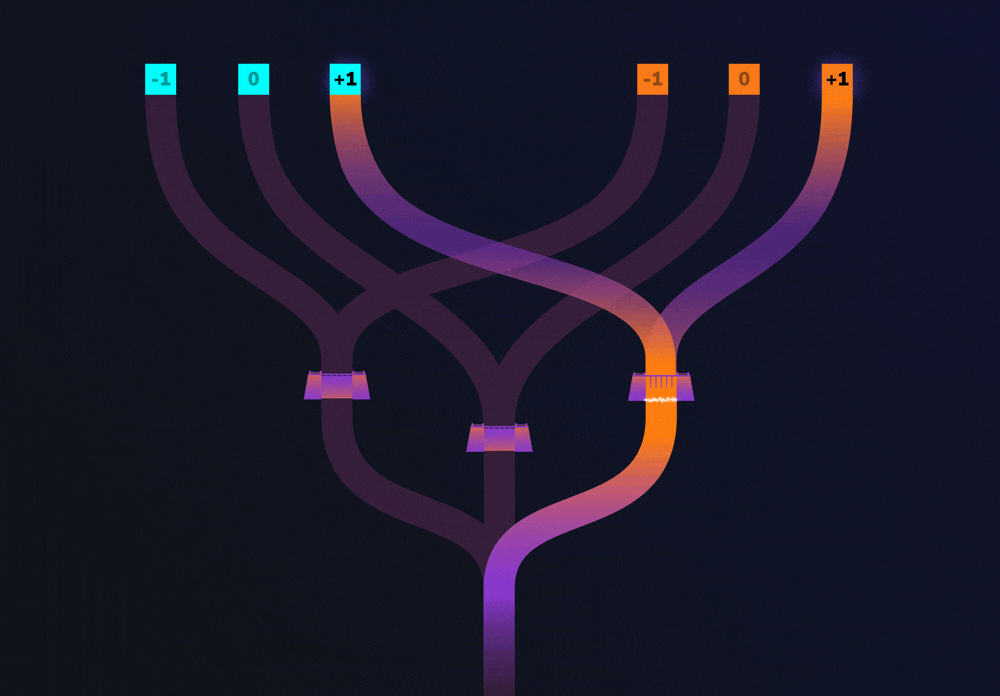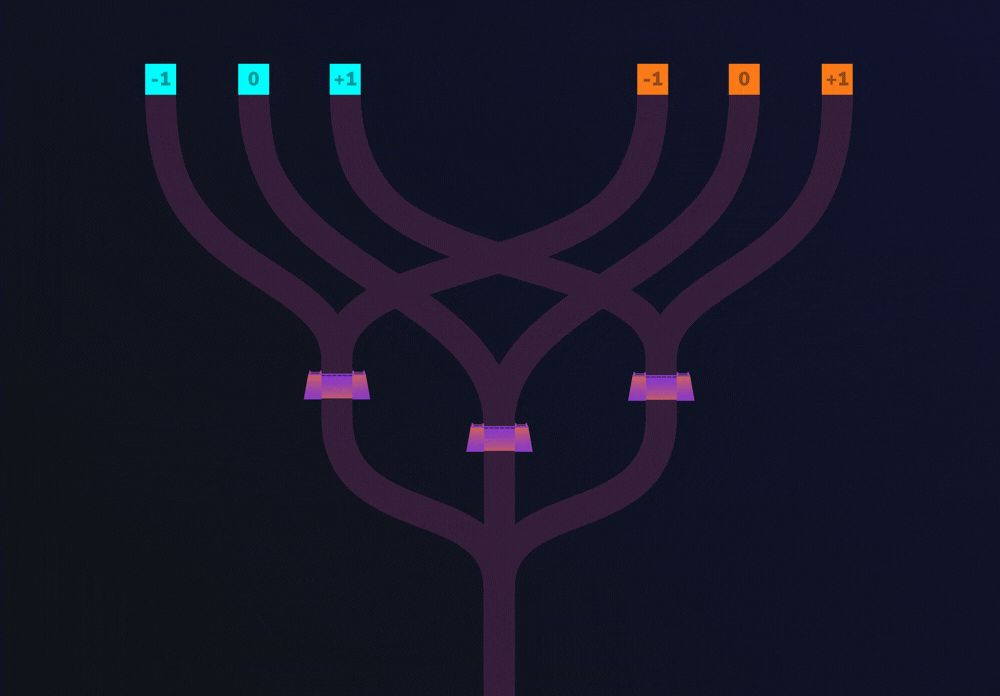
Now let’s see what happens when Alice pours water into the -1 trit of the cyan entrance and the 0 trit of the orange entrance. The channels from these entrances lead to different dams. If only one channel leads to a dam, there is not enough water to rise over the dam. So, we can say that when water does not rise over a dam, both input values were not the same (-1 and 0 in this case).
This flow represents a basic computation. The water that flows over the top of the dam is the result of the computation.
As long as Alice keeps pouring water into the same entrances, the result stays the same. For example, if the two input values are equal the water continues to flow over the dam and Alice sees the result. To then compare different values, Alice must stop the water flow, go and fill her buckets in the sea, and then pour water into the new entrances.
On our beach, the dams play a vital role. They help to decide if two trits are equal, allowing water to flow over them only if they are equal. When water flows over the top of the dams, it ends up at the point where all three channels meet. This point is called the merger.
It is the merger’s job to pass on the result to something else, so that more work can be done on it. For example, you may say ‘if these trits are equal, then go and do the next stage’.
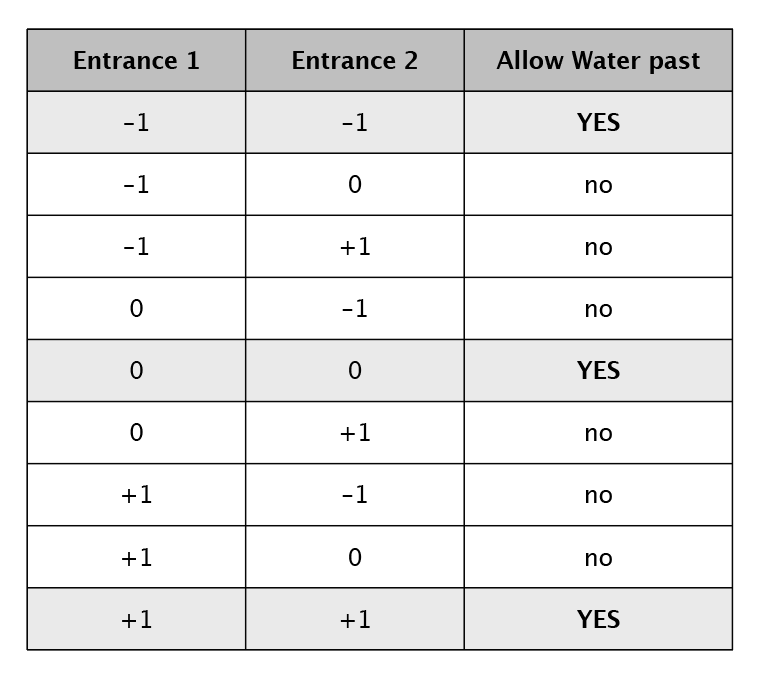
To help you see how this system works, here is a cheat sheet called a look-up table (LUT), that describes what happens to the water, depending on which entrances are used.
So let’s look at this LUT in action…
Note: you have control over this LUT. If you wanted to change the output, you could update the LUT. In this current form, both entrances must be equal for water to flow over a dam. But, what if you wanted both entrances to be unequal for water to flow over the dam? Well, we’d need to extend our example, which we will look at later in this article. But first let’s go over a few concepts.
First, the most important aspect. The fact that we can build QCM instances on a beach shows how simple it is. You need no extra components.
In traditional computation models, we would need more complex equipment to keep the water moving along the channels, and to get rid of hazards. This equipment would be more prone to failure and consume extra energy.
“In traditional computation models, we would need more complex equipment to keep the water moving along the channels, and to get rid of hazards. This equipment would be more prone to failure and consume extra energy.”
“In traditional computation models, we would need more complex equipment to keep the water moving along the channels, and to get rid of hazards. This equipment would be more prone to failure and consume extra energy.”
Therefore, this simplicity gives QCM its advantages in terms of energy efficiency and resilience (for example in harsh physical environments where complex elements are more prone to fail). But also this approach has the potential to overcome many of the major current problems in chip manufacturing (of clock skew, dark silicon, cross-talk, hazards, PVT variations and radiation susceptibility), though this is outside the remit of an ELI9 article.
On our beach, the only parts we need to do a computation are the channels, the micro dams, and Alice. Together the channels and the dams are called a branch, and Alice is called its Supervisor.
Our branch does only one type of computation, which checks two trits for equality. But, we could have made our branch more complex and extended it, for example to make a branch that checks if the trits are unequal as well.
In this example we have extended our branch, so now if the trits are unequal, the merger receives a result of -1. If the trits are equal, the merger receives a result of +1. Follow the lines on the diagram below to see for yourself.

Now, remember we said that you can update the LUT? We can reverse the output of this new LUT so that:
- If the trits are equal, the merger receives a result of -1
- If the trits are unequal, the merger receives a result of +1
These results can then be used in the next step.
What happens if Alice needs a break and doesn’t want to forget her result?
It’s lunchtime, and Alice wants to go and sit with her family. But, she doesn’t want to forget that her last two trits were equal, nor does she want the merger to stop passing on her result. So, she decides to use her water cooler.
Now that Alice has a source of water, she needs a way to direct it to the merger. To do so, she digs a direct channel from her water cooler to the merger.
Together, the water cooler and the channel that connects it to the merger are called a memory latch. A memory latch helps Alice not only to store her result, but also saves her from continually pouring water so that the merger keeps passing the result to ‘the next step’.
To keep things simple, let’s go back to our original branch that checks only for equal trits.
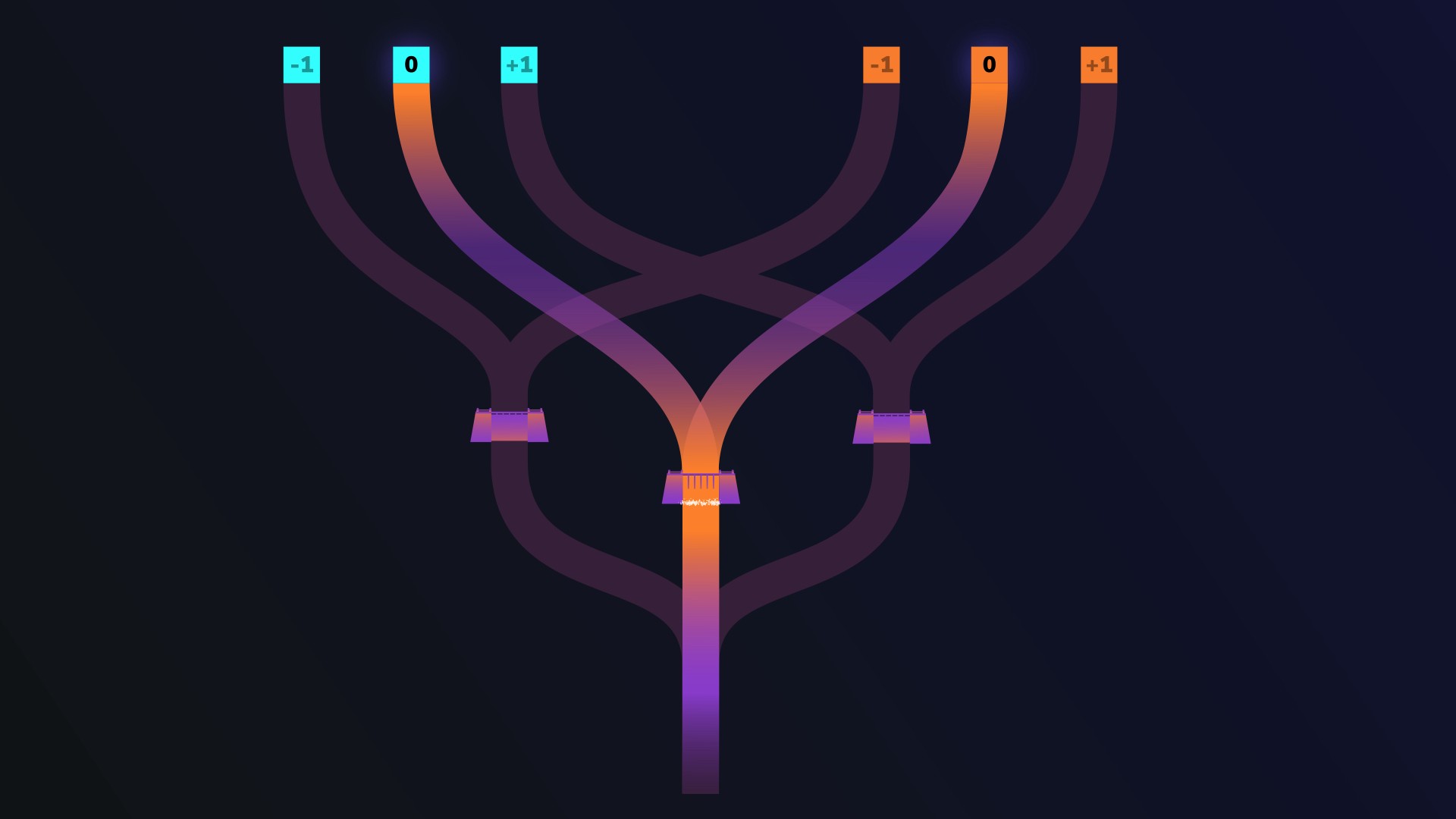
In our branch, Alice pours water into two entrances, which flow in one direction, down the branch and towards the merger. This branch outputs a single trit (+1 for equal), which is the result of our computation.
In the QCM, Alice is called the Supervisor. Alice is the key to QCM’s simplicity. Alice (the Supervisor of the branch) does the heavy lifting while the branch itself can be kept very simple, making it hardy to external factors. In fact some branches do not need their own Supervisor, and can use the outputs of other branches to regulate their flow.
“Alice is the key to QCM’s simplicity. Alice (the Supervisor of the branch) does the heavy lifting while the branch itself can be kept very simple, making it hardy to external factors.”
“Alice is the key to QCM’s simplicity. Alice (the Supervisor of the branch) does the heavy lifting while the branch itself can be kept very simple, making it hardy to external factors.”
In a previous, more technical blog post, we describe the idea of entities, effects, and environments (EEE).
Our branch is an example of an entity. It is the entity’s job to do a computation with some input data. That input data is given to the entity by Alice, our Supervisor.
Alice takes data from another environment when something in that environment changes. This change is called an effect. An example of an environment could be any other branch and the change (aka effect) could be water flowing down an output.
This process is called a wave, whereby the Supervisor takes data from one environment and gives it to our branch as input, allowing it to flow through and end in a result.
As mentioned earlier, not all branches in QCM even need their own Supervisor. Any branch can receive data from a different branch’s Supervisor.
By keeping the data flow simple, QCM is cheaper and simpler to implement than traditional computation models.
You may remember, we said that QCM uses trinary. This is because trinary is more efficient than binary. Now that we’ve built our first branch in the sand, we can explain why it is more efficient.
On our beach, Alice has 2 entrances, each with 3 channels (total = 6 channels), which each take up space. To be more efficient, Alice’s goal is to use the least amount of space on the beach to do a maximum number of computations. Beach space isn’t cheap!
Each entrance in our branch accepts one trit at a time. So, Alice can use those six channels to do computations on any two-trit number (one for each entrance).
What would our model look like if we were to use the same number (6) of channels on a beach that used binary (0 and 1) instead of trinary (-1, 0, and +1)? Well Alice would need 2 channels per entrance (each bit has two possible values) and so we could have 3 entrances (2 channels x 3 entrances = 6). Therefore, she could use three entrances with these six channels, to do computations on any three-bit number.
This may sound like binary would be more efficient because we have a three-bit number instead of a two-trit number in the same space, but let’s take a closer look.
In trinary, one trit can have one of three possible values: -1, 0, or +1. On our beach, Alice can enter two trits. This results in 3² (=3x3) possible combinations, which gives her 9 possible values. Note this matches the 9 possible combinations on the LUT we described earlier. So, Alice can use the6 channels to process9 values from a two-tritnumber.
In binary, one bit can have one of two possible values: 0 or 1. On our binary beach, Alice can enter three bits. This results in 2³ (=2x2x2) possible combinations, which gives her 8 possible values. So, Alice can use the6 channels to process8 values from a three-bit number.

By using trinary instead of binary, Alice can use the same space and the same six channels to process numbers that have a maximum value of 9 instead of 8. This saving helps Alice to do the most amount of computations in the least amount of space.
Although a 1/8 improvement (9 values instead of 8) doesn’t look significant, it makes our computations much more efficient. And this efficiency is more obvious when we start doing complex computations like multiplication or evenAI.
Note: 4-ry is not more efficient than 3-ry (trinary). If we took 12 channels we would get three 4-ry numbers giving 64 values (4³)or four 3-ry numbers giving 81 values (3⁴). Again we see that trinary is more efficient. Indeed, any other N-ry would be even worse than 4-ry.
We have shown above how we can keep data flows simple with QCM. This is key to keeping chip manufacturing both simple and cheap, and means that the circuitry will be able to withstand more extreme environments.
We have also shown how the use of trinary can further improve the efficiency of the system.
When applied at a large scale, this change has the potential to have a significant impact on the world of computing.