The Many Faces of the Tangle

A look at different Tangle behavior.

The Tangle is a complex mathematical object. It has a random structure defined by a separate random agent: the random walk. This makes its study challenging, but also very interesting. In order to systematically study the Tangle and its associated problems, we must first understand its structure.

This post presents a brief introduction on the different behaviors we expect from the Tangle depending on alpha, the parameter of the random walk, especially considering the number of tips and of stability its structure over time.

In this post I assume the reader has knowledge on what is the Tangle, how the random walk is used to select tips and what reattachment is. Alon Gal’s post about alpha and randomness is also recommended.

Recurrence and transience are terms widely used in probability theory. Here I will give some context on what those terms mean for the Tangle.

Unapproved transactions in the Tangle are called tips. Ideally we would like to have every transaction approved, so no tip is permanent. Denote by L(t) the number of tips at time t:

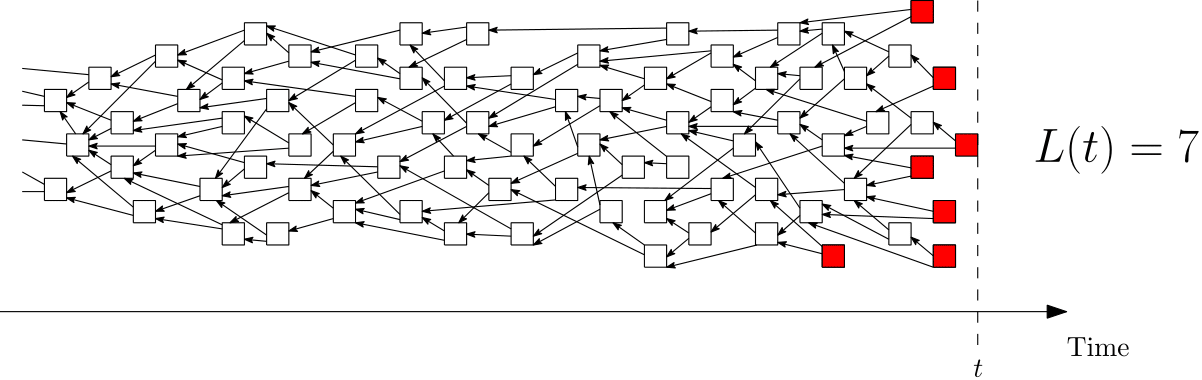
One example of Tangle with the value of L(t).

Now that we have this quantity, we can check how it behaves over time. Here are some simulations made by Bartosz Kusmierz:

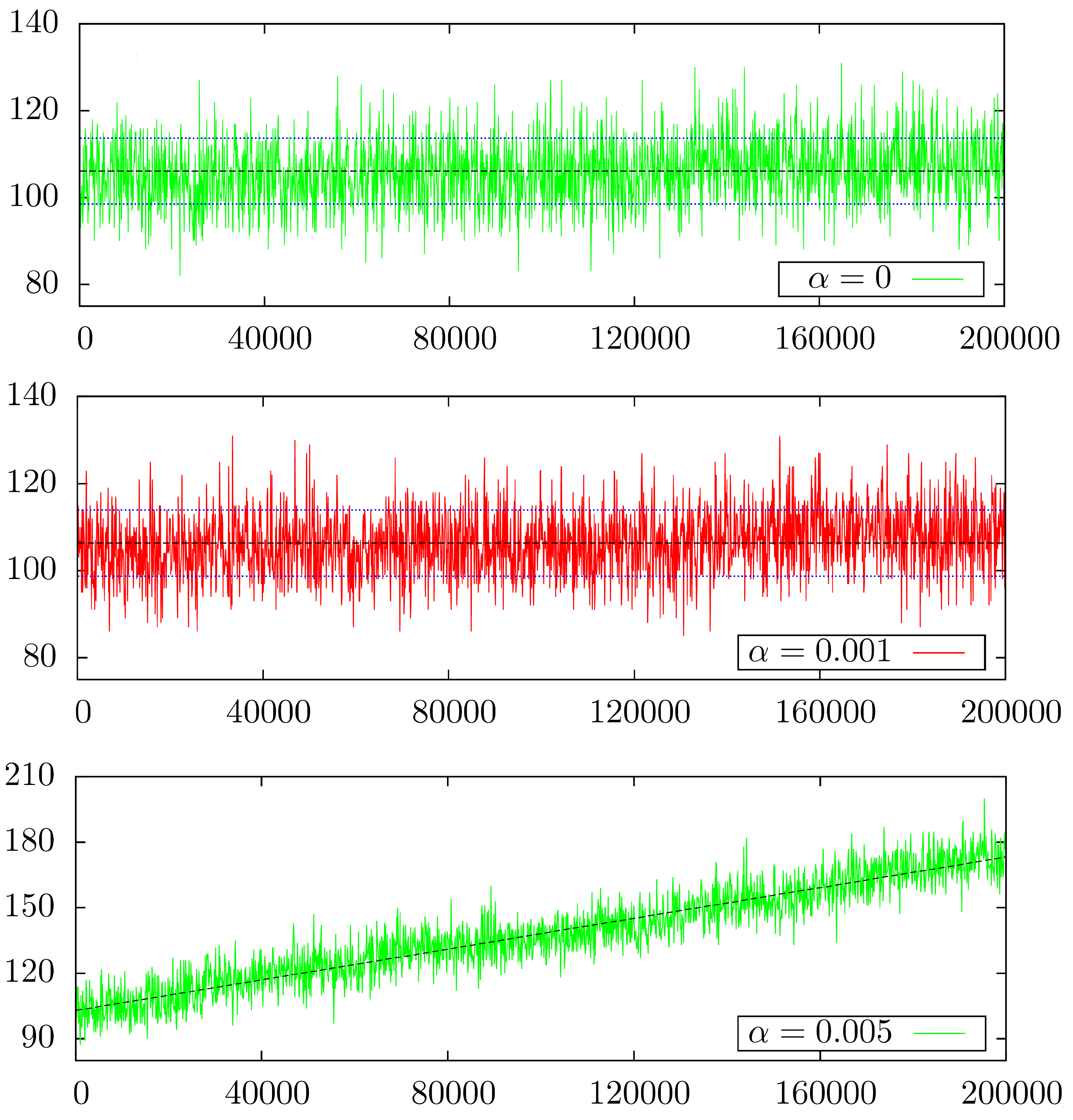
The behavior of L(t) over time for three different values of alpha over 200,000 transactions. For α=0.001 the slope of the average is so small that is not visible with just 200,000 transactions. Observe that for α=0.005 under 0.1% of the transactions are tips by the end.

The behavior of the number of tips with α=0 is the most desired one: the number of tips varies over time but it stays bounded, not growing on average. The other values of alpha have a less ideal behavior: the number of tips grows on average over time (for α=0.001 this is only visible after a huge number of simulations, so the graph is a bit misleading). Recurrence and Transience are names to specify exactly those behaviors. If we want to formalize it, we would have the following

The number of tips L(t) is recurrent for a tip selection if the average number of tips over time stays controlled (bounded).

The number of tips L(t) is transient for a tip selection if the average number of tips over time grows with no bounds.

The number of tips L(t) is transient for a tip selection if the average number of tips over time grows with no bounds.

Ideally, we want to always have a recurrent Tangle (we will say this to refer to a recurrent number of tips) as we don’t want unapproved transactions, but real life is not so forgiving. Simulations and some theoretical results suggest that the following holds

For α=0 the Tangle is recurrent (proved).

For α>0 the Tangle is transient (conjecture supported by simulations).

For α>0 the Tangle is transient (conjecture supported by simulations).

This means that we actually do not expect to have a recurrence for practical uses of the Tangle, and the number of tips will grow! Is this a problem?

Is the number of tips growing over time a problem? Naturally, a large number of left-behind transactions is not ideal. However, the Tangle employs a very small alpha value, making the growth of the number tips quite slow, so the few transactions that get left behind just need to reattach.

The behavior we want is the Tangle growing in a stable way, with no recent transactions approving old ones. We call this asymptotic stationarity, or simply stationarity. This means that after some time, the Tangle’s structure will no longer depend on its distant past. This implies that a transaction will quickly become approved or abandoned. This behavior is desired, as the user can quickly decide whether a re-attachment is necessary.

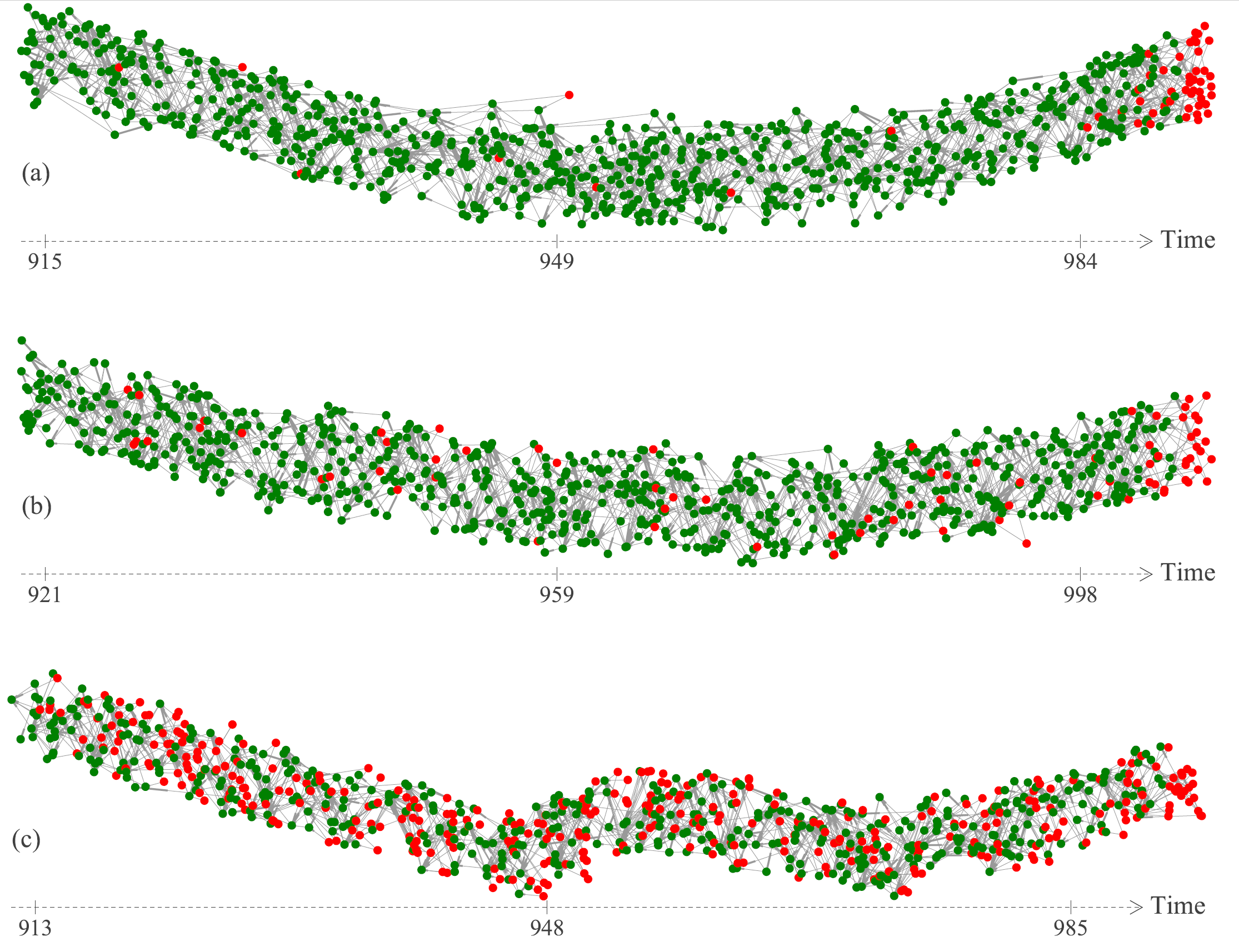
of the Tangle by Bartosz Kusmierz using (a) α = 0.05, (b) α = 0.1 and (c) α = 0.5. The large values of alpha make the Tangle leave many transactions behind, but it still grows in a stable way, with no recent tips approving old transactions.

This is possible even with transience! What happens is that even though we have transactions getting left behind, the exponential function of the random walk decreases the probability of approving these transactions over time, so the majority of probability is concentrated within the most recent tips. This keeps recent transactions from approving old ones and contributes to the good behavior we aim for.

The value of alpha affects the Tangle’s behavior in many ways. For any positive alpha we have transience, but this does not affect stationarity and consequently, the Tangle is kept stable over time. Furthermore, for positive alpha, the number of tips is slowly increasing in time, which, in practice, implies that occasional reattachments are necessary.

Finally, we should remember that alpha plays a role of security against lazy tips and parasite subtangles, so research about alpha tries to discover how small alpha can be allowed to be, while maintaining the security attributes of the Tangle.