Attack Analysis - the Simple Parasite Chain

Note: This blog post is intended for a reader with a basic understanding of the Tangle. In particular, we heavily rely on concepts like a random walk in the Tangle, a cumulative weight (and how it affects random walk), an α parameter, and a parasite chain attack. We recommend reading the IOTA Whitepaper first (especially section 4), click here. It is also recommended to read Alon Gal’s blog post on the α parameter.

IOTA, unlike first-generation distributed ledgers, is not based on a blockchain, but rather on a directed acyclic graph (DAG). This novel architecture brings numerous advantages. The most emphasized of which are scalability and no mining fees. However, with a new approach to managing the ledger comes the fundamental question of the security of the new solution. In this blog post, we partially answer this question, by providing a brief introduction to the parasite chain (PC) attack, proposed in the Tangle white paper (subsection 4.1). This topic is an active area of research in the IOTA Foundation.

The parasite chain attack is an attempt to double spend funds in the tangle based on the following idea:

The attacker secretly builds a sub-tangle, invisible to the public. We will call this sub-tangle the “parasite chain”, or PC. At some point, he/she issues a transaction in the main tangle (MT), buying some commodity from a merchant. The attacker has already constructed a conflicting transaction on the PC (which moves the money to one of the attacker’s accounts, instead of the merchant’s) — therefore they have created a double spend transaction.

Since the conflicting transaction in the PC is hidden, after some time the merchant accepts the payment on the MT. The attacker then hopes to “invalidate” this transaction by broadcasting the PC to the public.

The PC is built to exploit the tip selection algorithm and make most of the incoming transactions approve the double-spend transaction from the PC. If successful, this action effectively changes the past and invalidates the “good’” transaction that the merchant had accepted. It is worth noting that a successful attack results not only in stealing goods from the merchant but also causes collateral damage — all “innocent” transactions that approve the fund transfer to the merchant’s account, are invalidated.

An analysis of a general PC is very complicated since PCs come in all shapes and sizes. The attacker has the freedom to choose how many transactions from the PC approve transactions from the MT, and which transactions the attacker should approve. What is the optimal relative position of transactions in the PC? Should it even be a chain or some other more efficient structure? All of the above are important and challenging questions because they involve a huge number of degrees of freedom. With this disclaimer in mind, in this blog post, we will not try to perform a general analysis, but rather focus on one specific example of a PC. We present data for the so-called simple parasite chain(SPC). As we will show, despite its simplicity, the SPC possesses interesting and in many ways surprising properties. We decided to analyze this particular chain first because in many ways it is the most natural.

Let us define the SPC:

A simple parasite chain is a sequence of transactions where each transaction directly approves:

1) The previous transaction from the SPC
2) A specified MT transaction which we call r

One of the SPC transactions is in conflict with a certain MT transaction. It is important for rto be placed before the MT double-spend transaction. Otherwise, the PC transactions would all be invalid. We illustrate SPC in fig. 1.

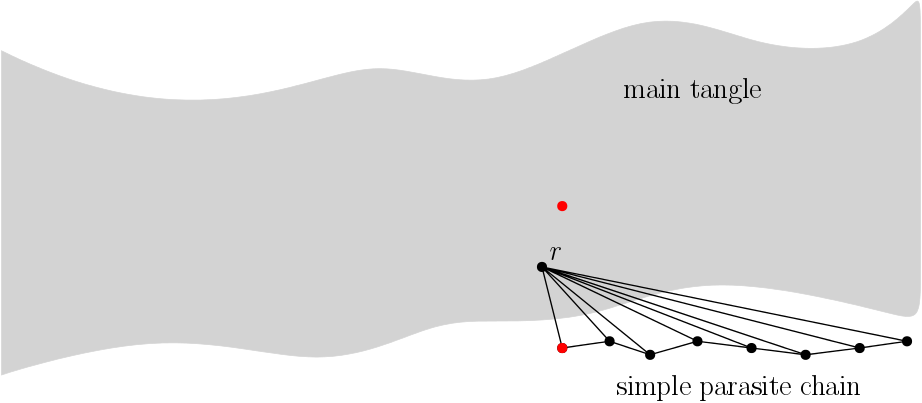
We want to focus on the following quantity: the probability that an arbitrary random walk reaches the final transaction of the SPC. If this happens for the majority of incoming transactions, it means that the attack is likely to succeed. Honest users of the network will prefer the PC over the MT, when in conflict.

One of the methods we used to estimate this probability was a simulation where we simply run a large number of random walks and count how many of them reach the SPC. Before we show the results, we want to stress that this quantity is not the same as the success rate of attack. In order for an attack to be successful, the majority of incoming transactions have to approve the SPC, and thus make it the dominant sub-tangle. If the probability that an arbitrary walk will end up on the SPC is 10%, the probability that the attack will be successful is still tiny and the only harm to the Tangle is that 10% of otherwise valid transactions attached to the SPC will be orphaned (it does not mean that funds from those transactions will be lost, but that those transactions will have to be re-attached). An attack could actually be threatening when the analyzed probability is close to or above 50%.

We now present simulation data for an attack scenario where the attacker has a very significant percentage of hashing power. We look at that arbitrary particle will reach the SPC as a function of the αparameter.

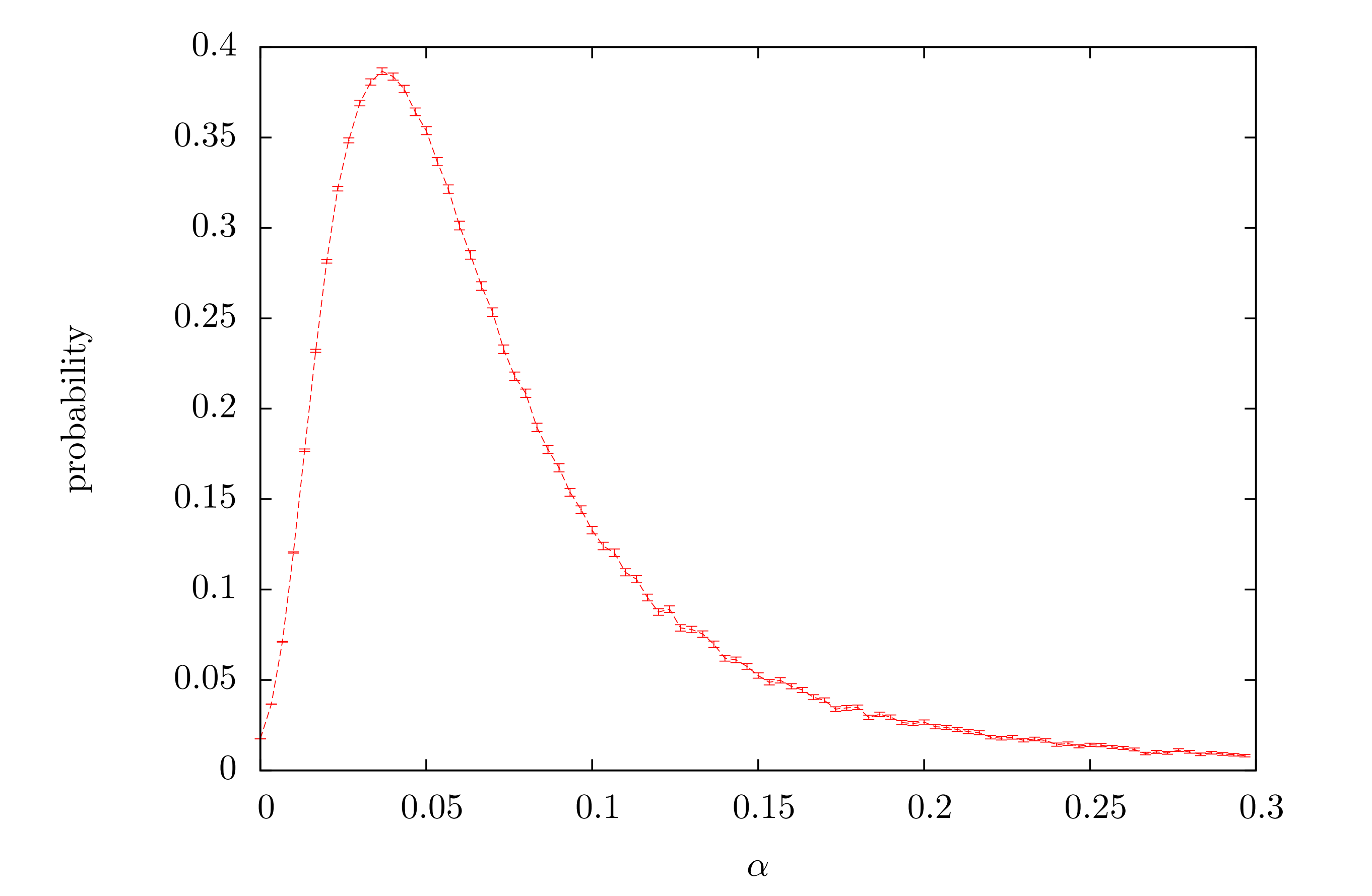
Figure 2: Probability that an arbitrary walk will end up on the SPC as a function of α. There are 400 transactions in the MT and 100 transactions in the SPC, implying the attacker has 20% of the total hashing power

The presented data reveals a local probability maximum. This is somewhat surprising because as α grows it makes particles stick to the heavier part of the Tangle: the MT. Having this in mind we were expecting monotonically decreasing probability. However, this naive picture turned out to be only a part of the story.

The probability distribution tells us that there are at least two competing “forces” at play. To discuss them, let us specify two conditions that must be fulfilled for the walk to end up on the PC:

a) The walk has to pass through r,
b) The walk has to hop from r to the PC.

No doubt it is true that asαgrows the probability of event b)decreases. However, event a) becomes more probable asαgrows.

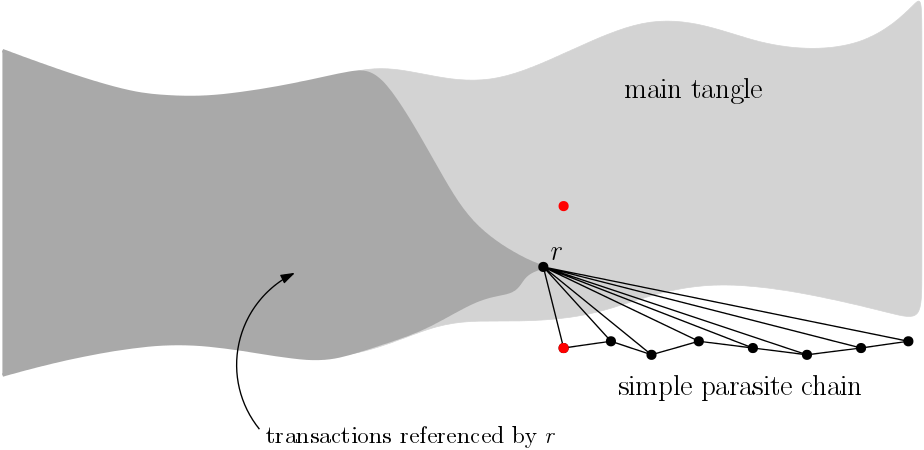
This is due to the fact that the cumulative weights of transactions from the PC “attract” random walks to transactions referenced by the PC. The strength of this attraction grows with α. In the case of the SPC attack, where the PC is attached to one single transaction r, we have the following situation: on the one hand, the walk wants to stay in the region with additional cumulative weight (see fig. 3 - dark gray area), but on the other hand, it drifts to the end of the tangle. Since r is at the end of the gray area, walks tend to pass through it.

and acquire additional cumulative weight from the SPC.

Let us go back and examine the probability of event b). We used an analytical calculation to estimate this value. Fig. 4 shows the values of this analytical expression for some example parameters.

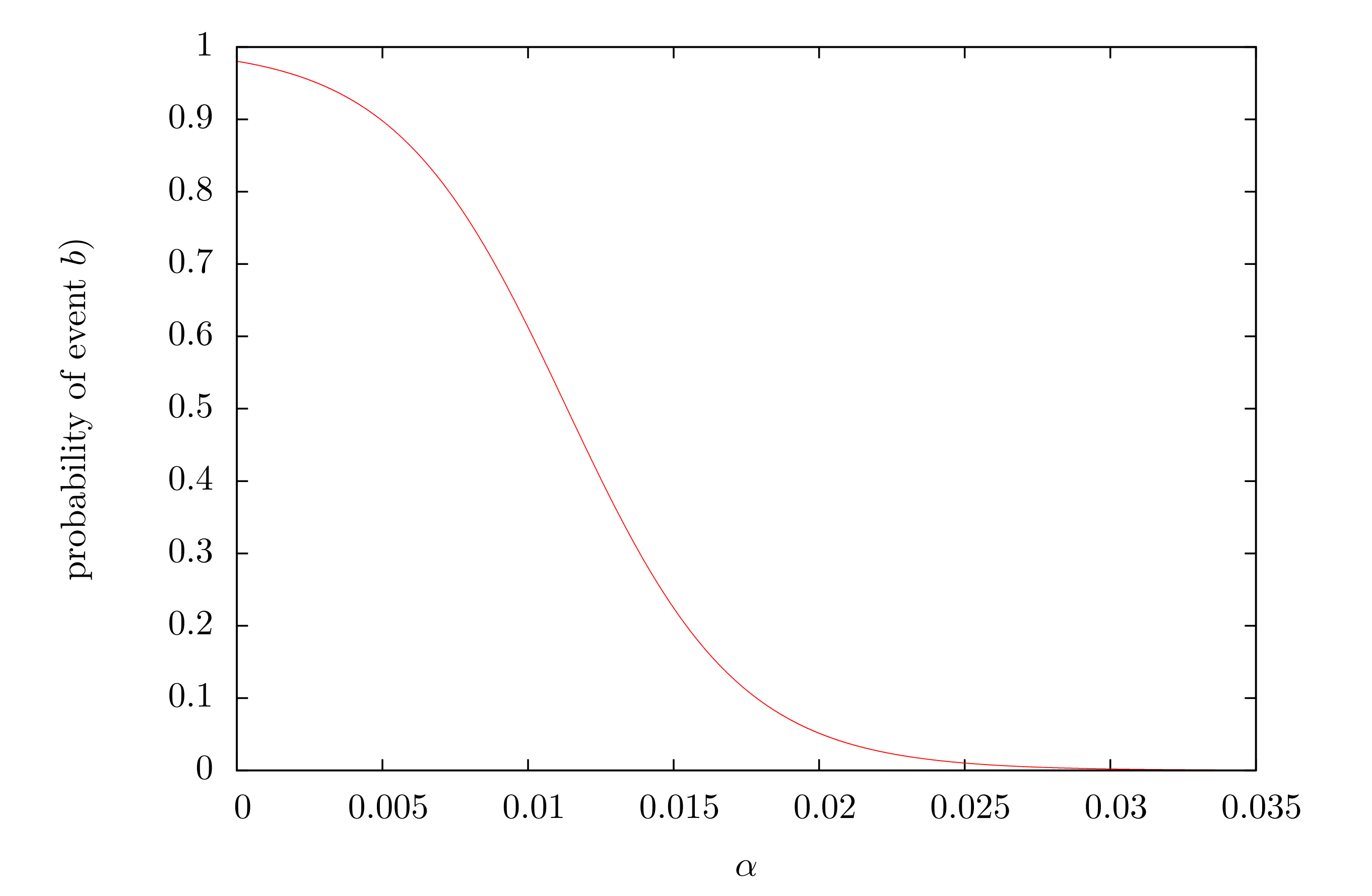
for 400 transactions in MT and 100 transactions in SPC.

In essence fig. 4 visualizes the security level (the probability of random walk hoping to the PC) as a function of α. It should be noted again, that this is not the probability of an attack to be successful but only for event b)to happen. Nevertheless, it is an important indicator of safety. We can also invert this function. The inverted function would give the α, which is required to assure that the security level is above a given level p. Fig 5. shows a heat map of the resulting alpha value for a selection of sizes of the MT and the SPC, where the safety level was required to bep=0.1.

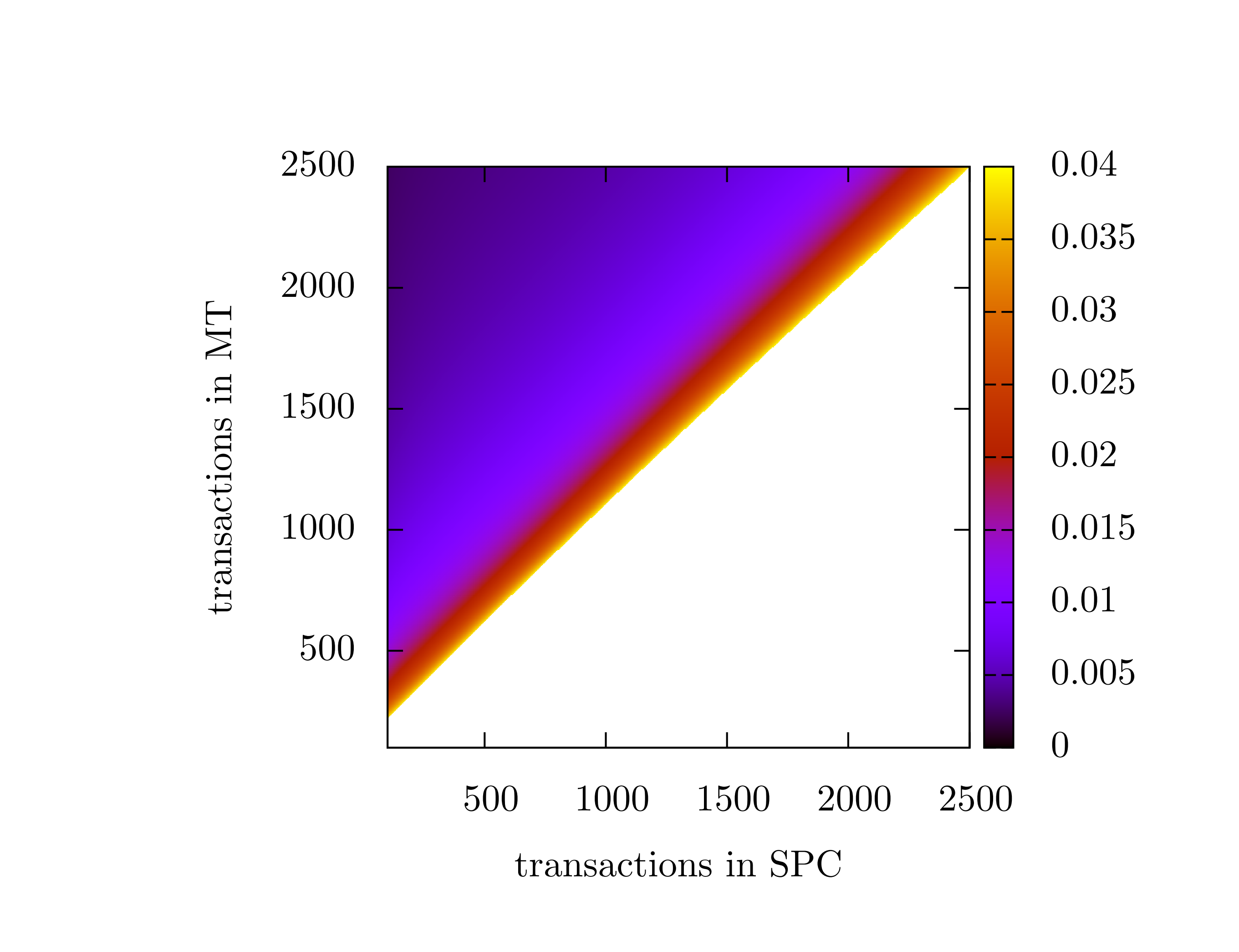
Figure 5: The value of α presented on a graph provides the p=0.1 probability that particle will reach the SPC, for different sizes of SPC and MT. The plot is valid when a number of transactions in the MT is bigger than in the SPC.

In this blog post, we examined the simple parasite chain attack and some of its interesting properties. Most notably, we saw that there is an “ideal”αfor this type of attack, where it is most effective, which is a non-trivial result. While the SPC is probably not the most efficient way to attempt a double spend, it is an important baseline. We can use it to define a lower security bound forα, and for comparison against future more sophisticated attacks. In the future, we will release a report on the security in the Tangle, where we’ll provide more simulation data, derive all of the formulas, and discuss our methodology.

For further reading on the Tangle we recommend: